Why 19th-century mathematicians were obsessed with coloring maps
Have you read Mark Twain’s Tom Sawyer Abroad? There’s this part where Tom says:
“Suppose there’s a brown calf and a big brown dog, and an artist is making a picture of them. What is the MAIN thing that artist has got to do? He has got to paint them so you can tell them apart the minute you look at them, hain’t he? Of course. Well, then, do you want him to go and paint BOTH of them brown? Certainly you don’t. He paints one of them blue, and then you can’t make no mistake. It’s just the same with the maps. That’s why they make every State a different color; it ain’t to deceive you, it’s to keep you from deceiving yourself.”
So, how many colors do you need to color a map in a way that no two adjacent regions have the same color?
The question may look deceptively simple, but when it was first raised in 1852, it became one of the most famous challenges in the history of mathematics. A famous British mathematician of the 19th century, Augustus De Morgan, wrote to a colleague that one of his students believed only four colors were needed to color any map. Not five. Not six. Not more. Only four.
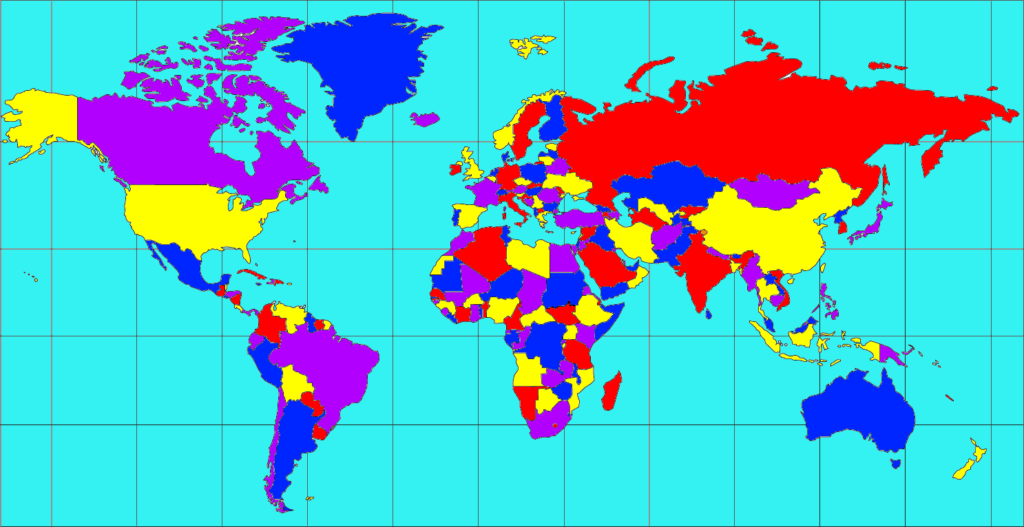
“He says that if a figure be any how divided and the compartments differently colored so that figures with any portion of common boundary line are differently colored—four colors may be wanted but not more,” De Morgan wrote in his letter.
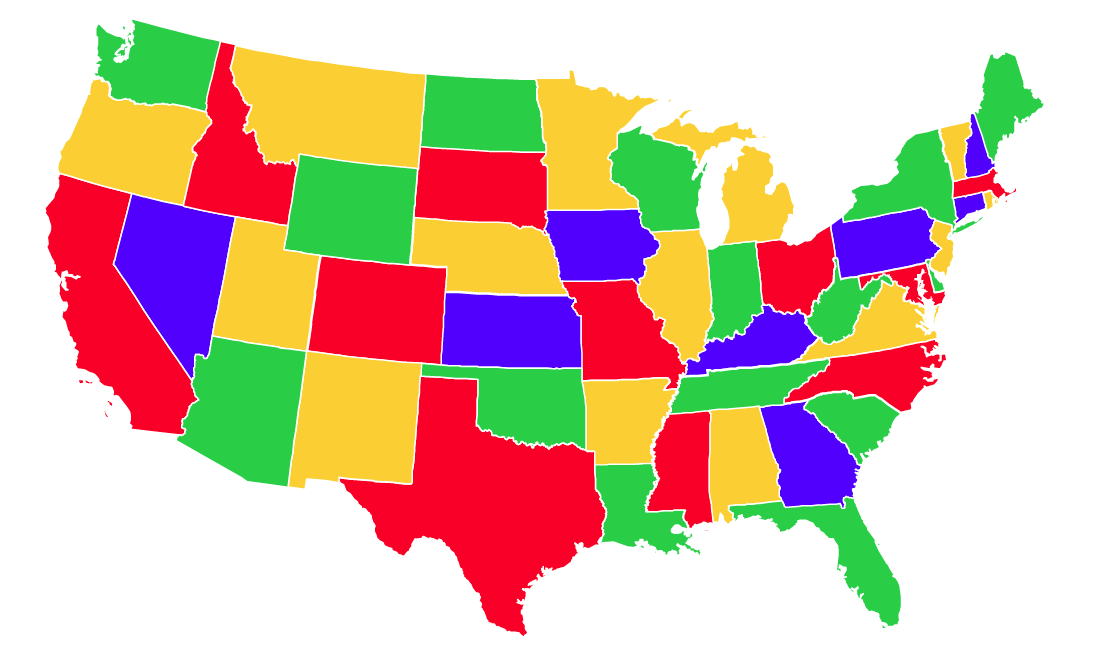
This map could be on a plane or a sphere – and it could be a map of the real world or any fictitious graph. In the four color theorem, two regions are called adjacent if they share a common boundary that is not a corner. And corners are the points shared by three or more regions. So, this theorem doesn’t require you to worry about divided states (like Michigan in the United States) because single points are not counted as borders.
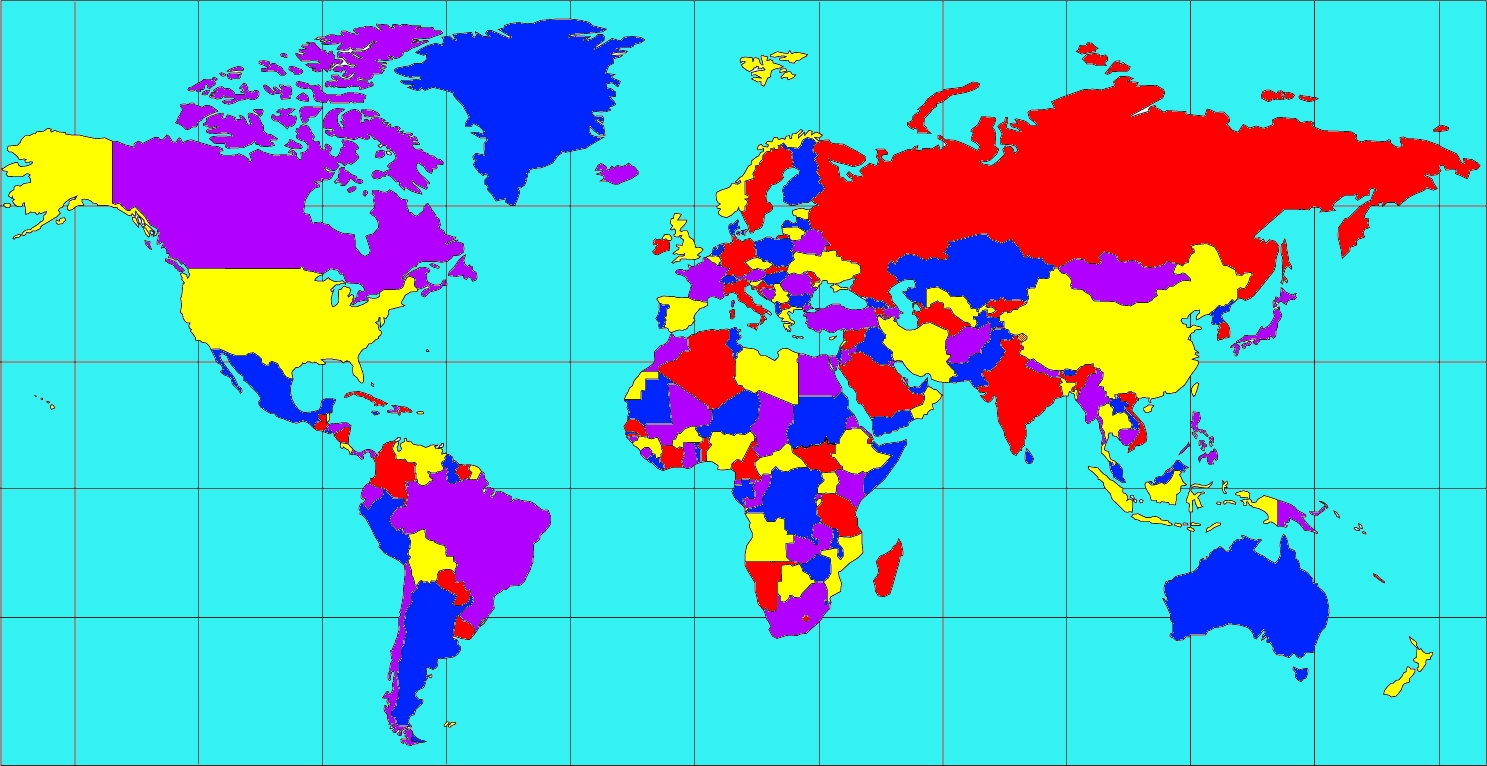
Even then, the question remained: Was there any map which necessitated the fifth color despite fulfilling these conditions? The conundrum sent everybody from amateur number crunchers and professional mathematicians to astronomer Lewis Carroll and the Bishop of London on a quest to find the answer.
The cartographic community, meanwhile, couldn’t care less. At a time when the British had dominance over much of the world, mapmakers had bigger problems to worry about, like should all Brit-occupied regions have the same color?
So, the cartographers continued dipping their masterpieces in varied hues while mathematicians painted maps on doughnuts and horseshoes and played with patterned soccer balls and the great rhombicuboctahedron in their pursuit of the solution. In his book Four Colors Suffice, mathematician Robin Wilson even describes how a bridegroom spent his honeymoon coloring maps!
For years, the problem baffled the greatest of mathematicians as they worked on the ‘proofs’ of the concept. In 1879, a proof by Alfred Kempe was published in the American Journal of Mathematics and everybody thought that was that. Until 1890, when another mathematician, Percy John Heawood, demolished it. Wilson writes about Kempe’s proof in his book, “It was incorrect, but it was a very good incorrect proof. Not only did it convince Victorian mathematicians for eleven years, but most of the ideas it contained were sound and would form the basis for later assaults on the problem, including the one that was ultimately to prove successful.”
 The one that ultimately proved successful came countless colored maps and 125 years later. In 1976, two mathematicians from the University of Illinois, Kenneth Appel and Wolfgang Haken, proved the theorem by basically by showing all possible kinds of graphs that could be contained in a map (more than 1,900) and then coloring them successfully with just four colors.
The one that ultimately proved successful came countless colored maps and 125 years later. In 1976, two mathematicians from the University of Illinois, Kenneth Appel and Wolfgang Haken, proved the theorem by basically by showing all possible kinds of graphs that could be contained in a map (more than 1,900) and then coloring them successfully with just four colors.
Naturally, it was too tedious a task to have been accomplished by just two humans. The four color map theorem went down in history as the first math problem to be solved with the help of a computer, using no less 1,200 hours in supercomputer time. Of course, now we use computers for math problems, but at that time the academic community wasn’t too thrilled to see this controversial method in use.
“Many mathematicians and philosophers claimed that the proof was not legitimate,” the University of Cambridge recounts. “Some said that proofs should only be ‘proved’ by people, not machines, while others, of a more practical mind questioned the reliability of both the algorithms and the ability of the machines to carry them out without error.”
Whatever the opinions expressed, the four color map theorem is not only important for being one of the most perplexing math problems of all times, but also because it has practical real-world applications. Take cell towers, for example. The principle that governs the theorem also stipulates that if you use four different sets of frequencies, no two adjacent towers will need to use the same frequencies.
If you want to learn more about the four color theorem, watch this fantastic video by Numberphile below: